There's a new word game on the Internets. And the past week, there have been cryptic grids of black, orange, and green tiles all over my Twitter timeline.

Wordle is a daily word game, somewhere between a crossword puzzle and Scrabble.^[1] Every twenty-four hours, there's a new "word of the day", and you get six tries to guess what the word is.

After each guess, the game tells you how close your guess was to the correct word.

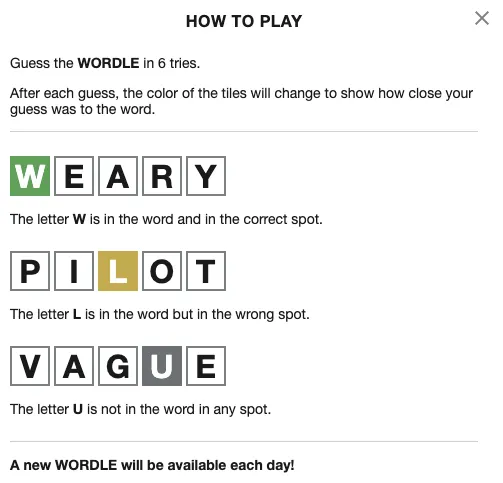
I played the game a few times. (It's really fun.) And it got me thinking about how a program that can solve the puzzle might look. So, here goes. Here's how to build a Wordle solver.

Sound guesses ​

As you might expect, the aim of the solver is the same as with a human player: try to guess the correct word in six or fewer tries. To see how it can do that, we'll study a few scenarios and then build our way up to a general solution.

Say we have a game where the correct word is "STARS". If we try guessing "RADAR", we'll see this result:

What does this tell us about the correct word?

The "R" in the first position of the guess is marked yellow, while the one in the fifth position is grey. So, we know there's an "R" in the correct word, and it's not in the first position. Because the second "R" is grey, we also know that there is no other "R" in the word. (We can also tell that there's no "R" in the fifth position, but we'll see why in the next example.)

We can make a similar conclusion for "A": there's only one "A" in the correct word. And it's not in the second or fourth position. Finally, we can tell that there's no "D" anywhere in the right word.

Alternatively, if we guess "FRERE" instead, we'll see this result:

As before, we can conclude that the correct word has no "F" or "E". We also learn that it has a single "R" in the fourth position.

Note how the result highlights the correctly placed "R" first, instead of the wrongly placed "R". That's why we could tell from guessing "RADAR" that there's no "R" in the fifth location and no "A" in the fourth position.

Each guess we make tells us more about the correct answer. But not always. If we don't use what we learned from the result of the previous guess, we'll learn nothing new in the next guess.

For example, if the correct word is "BEBOP" and we guess "NAILS", the result would show that our guess has none of the letters in the answer. "SNAIL" would be a poor next guess. But "THREE", which has none of the same letters as "NAILS", would be much better.

So, we want each guess to use all the information from the previous result. We'll call guesses like these sound guesses and guesses that make the same mistakes as the last guess unsound. Unsound guesses use up the number of tries without getting closer to the correct answer.

From the examples we discussed, we can say that a guess is sound if:

1. it has all the correctly guessed letters in the previous result in the same positions
2. it has each of the misplaced letters in the previous result in a different position from where we last guessed it
3. if it has a letter marked as wrong in the previous result, the letter occurs p+q times in the guess, where p is the number of times the letter was correct, and q is the number of times the letter was misplaced

The third rule looks a bit more daunting than the first two. Remember the example where the correct answer was "STARS", and we guessed "FRERE"? The first "R" was wrong, while the other "R" was correct. If the result shows a letter as wrong, it doesn't mean the letter doesn't occur in the correct answer at all. But that it doesn't occur any more times after it was correct or misplaced. In the case of "FRERE", a word with zero or two “R”s would be an unsound next guess, while words with a single "R" in the fourth position would be sound.

We can figure out which words are worth considering for the next guess with these three rules.

The soundness checker ​

We'll define a function, getSoundGuesses(), that filters a dictionary of words for sound guesses based on the result of the previous guess.

// Returns the words that pass the checks based on the result of the guess
function updateGuessResult(words, guess, result) {
  // Get the values of `correctLetters`, `wrongLetters`,
  // `misplacedLetters`, `numMisplaced`, and `numCorrect`
  // by comparing the guess and result

  return words.filter((word) =>
    isSoundGuess(
      word,
      correctLetters,
      wrongLetters,
      misplacedLetters,
      numCorrect,
      numMisplaced
    )
  );
}

Inside isSoundGuess(), we'll implement the three rules for checking if a word is a sound guess.

For rule 1:

// `correctLetters` is a map of the index of each correctly guessed letter to its value

// For each index in the word...
for (let i = 0; i < word.length; i++) {
  // If we've already correctly guessed the value of this index, and
  // this word does not have that correct value, we can discard the word
  if (correctLetters.has(i) && correctLetters.get(i) !== word[i]) {
    return false;
  }
}

Rule 2:

// `misplacedLetters` is a map of the index of each misplaced letter to its value

// For each index with a misplaced value
for (const [index, value] of misplacedLetters) {
  let hasMisplaced = false;

  for (let i = 0; i < word.length; i++) {
    if (word[i] === value) {
      // If the word has the misplaced value
      // in the same index, we can discard it
      if (index === i) {
        return false;
      }
      hasMisplaced = true;
    }
  }

  // And if the word does not have the misplaced
  // value *at all*, we can also discard it
  if (!hasMisplaced) {
    return false;
  }
}

Rule 3:

// `wrongGuesses` is a map of the index of each wrong letter to its value
// `letterCounts` is a map of each letter in this word to the number of times it occurs in this word

// For each wrongly guessed letter...
for (const letter of wrongLetters) {
  // If the word includes this letter...
  if (word.includes(letter)) {
    const numLetterOccurs = letterCounts.get(letter);

    // It should only occur exactly the sum of the number of times
    // it was guessed right (whether in the right or wrong position)
    if (
      numLetterOccurs !==
      (numCorrect.get(letter) || 0) + (numMisplaced.get(letter) || 0)
    ) {
      return false;
    }
  }
}

If all three checks pass, then the word is a sound guess:

return true;

We now have a way to check if a word is a sound guess based on a previous result. Given a dictionary of all five-letter words, getSoundGuesses() can tell us what words would not be a total waste of time for the next guess.

That's all good and fine, I hear you say, we know what we can guess, but we still don't know what we should guess. If we have only one sound guess, we can use it immediately. But more often than not, we'll have more than one word that satisfies the rules of the previous result.

A naive approach could be to pick one of the sound guesses at random. But we have only six tries to find the correct word; we'll have to do a little better than that. We'll need a scoring system.

Scoring words ​

What makes one word a better guess than another?

We can look at this problem in information terms: a sound guess is better than another if it is more likely to provide more information about the correct answer.

A perfectly-good guess provides complete information about the correct word (it tells you exactly what it is!). And a perfectly-bad guess gives zero new information about the answer; guessing the same wrong word twice, for example, gets you no closer to finding the solution.

In other words, a perfectly-good guess reduces the number of sound guesses in the next turn to one, while a perfectly-bad guess leaves the number of sound guesses in the next turn unchanged. To generalize, we can say that a guess is better than another if it is more likely to make the set of sound guesses in the next turn smaller.

Let's consider a few examples. Say the Wordle board is empty, and you're about to make your first guess; which would you play: "QQQQQ" or "AAAAA"? (Both aren't real words; we're only using them to illustrate the point.)

Because "A" occurs much more frequently than "Q" in the English alphabet, guessing "AAAAA" is more likely to get you closer to finding the correct answer. If you guess "AAAAA" and the result says the correct answer has no "A", you can reduce your next search to the set of words that do not have A's (a much smaller set). And if the word has an "A", you learn the location(s) of the "A".

In contrast, by guessing "QQQQQ", you're likely to learn less. If "Q" is not in the correct answer (highly probable), you can only reduce your next search to the set of words that do not have Q's (which is still a large set).

That's one piece of the puzzle: a guess is better than another if it has letters that are more likely to occur in the correct word.

Here's another example: which is the better word to use as a first guess, "AAAAA" or "ALERT"?

Both words have frequently-occurring letters, but "ALERT" is a much better guess because it has different frequently-occurring letters. There's a higher probability that one of the letters in "ALERT" is in the correct word than with "AAAAA". By guessing "ALERT", we have a higher chance of learning the locations of those letters.

The quality of a guess is a function of the relative frequency and diversity of its letters.

The scoring system ​

Given a set of sound guesses, we'll first calculate the frequency distribution of the letters. And then find the word that returns the highest value based on the scoring function.

function getBestGuess(words) {
  // Assign scores to the letters in the set
  let letterScores = getLetterScores(words);

  let bestWord;
  let bestWordScore = Number.NEGATIVE_INFINITY;
  for (const word of words) {
    // Get the score of each word as a function of the
    // word itself and the frequency distribution of the letters
    let score = getScore(word, letterScores);
    if (score > bestWordScore) {
      bestWord = word;
      bestWordScore = score;
    }
  }

  // Return the word with the highest score
  return bestWord;
}

To get the scores for the letters, we'll first compute the frequency distribution of the letters in the set.

// Map of a letter to the number of times it appears in the list of words
const frequencies = new Map();
for (const word of words) {
  for (const letter of word) {
    frequencies.set(letter, frequencies.has(letter) ? frequencies.get(letter) + 1 : 1);
  }
}

Then we assign scores to the letters, from 0 to 25. We'll give the letter with the lowest frequency a score of 0 and the one with the highest frequency, 25.

let letterScores = new Map();

// Sort the letters by their frequencies (ascending)
sortBy(alphabet, frequencies.get).forEach((letter, i) => {
  // Map each letter to its score
  letterScores.set(letter, i);
});

To find getScore(), the score of each word, we first sum up the scores of all its letters:

let score = 0;

// Add the score of each letter in the word
for (let i = 0; i < word.length; i++) {
  score += letterScores.get(word[i]);
}

Then we'll add a score for the uniqueness of its letters.

const numUniqueLetters = new Set(word).size;
score += numUniqueLetters * UNIQUENESS_SCORE_WEIGHT;

return score;

(UNIQUENESS_SCORE_WEIGHT is the weight of the uniqueness score relative to the score of the letters' frequencies. A low value will prefer words with frequently-occurring letters, even if they repeat multiple letters; a high value will prefer words with unique letters, even if they have low frequencies. I found that a value of 5 works reasonably well.)

Finally, we can put it all together. At first, we'll get a list of all possible five-letter words.^[2] While the game hasn't ended, we'll get the best guess from the list, play the guess, and then update the word list based on the result.

let words = getDictionary();
let result; // result of the last guess

while (!isGameOver(result)) {
  const guess = getBestGuess(words);
  result = play(guess);
  words = getSoundGuesses(words, guess, result);
}

Performance ​

Here's how many guesses the solver needs to figure out these 12,483 words.^[3]

Words at the tail end of the chart, like "lills", take many tries to guess because many other words have similar letters. The solver tries guessing words like "bills", "fills", "tills", "hills", "wills", and "pills" before getting to "lills".

And…that's all. A few if statements and a for loop here and there. That's what it takes to make an "AI" player for Wordle.

If you enjoyed reading this, you might also like Building Ayòayò: An Unbeatable Player.