As long as humans have been around, we have been exploring: by curiously wandering into unknown wildernesses by foot; by sailing across seas to seek out distant lands; by sending high-speed spacecraft to investigate moons and planets billions of kilometres away.

At each step in the history of exploration, we required more technology than the previous one. Sea exploration depended on the invention of sailing ships. Space exploration needed the invention of spacecraft.

In particular, to explore distant space, spacecraft need enough fuel to travel long distances and a way to replace worn-out mechanical parts. John von Neumann, the Hungarian mathematician, physicist, and inventor, thought that the best way to maintain these far-travelling spacecraft was to make them self-replicating machines: machines that could create copies of themselves. Instead of waiting for spare parts from Earth, these machines would extract raw materials from planets and moons and manufacture replicas of themselves for further exploration.

Von Neumann shared these ideas for non-biological self-replicating systems in lectures he delivered in the late 1940s. But he found his models challenging to work with at the time. Instead, he went on to design an abstract representation of self-replicators based on cellular automata.

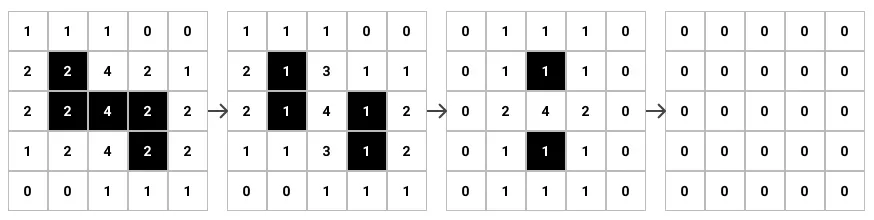
(A cellular automaton is a system of cells laid out in a two-dimensional grid. Each cell is a finite-state machine, having one of a predefined number of states at each turn. And at the next turn, each cell transitions to its next state based on the states of its surrounding cells.)

In von Neumann's cellular automaton, each cell could be in one of 29 possible states, and its next state was determined by the states of the cells to its north, west, east, and south.

With this model, von Neumann showed that a certain pattern of cells can make infinite copies of itself within the cellular universe. The pattern consists of two parts: the constructing machine and a line of cells that serve as a blueprint. The constructing machine reads the instructions from the blueprint one cell after the other and performs the corresponding actions, which result in an identical machine pattern.^[1]

Life ​

Years after von Neumann first proposed his universal constructor, the British mathematician John Conway read about his ideas. Conway found that von Neumann's implementation could be much simpler and that it didn't need to be explicitly programmed for self-replication. As long as the automaton's rules were sufficiently complex, self-replicating patterns would emerge.

John Conway started working on a new kind of cellular automata with simpler game rules. He played around with many different rules at first. Some led to patterns that were too chaotic and died off too quickly. Others led to patterns that were too static and didn't have any interesting behaviour. Until he found rules that fell somewhere in between. He called this system the Game of Life. Or Life, for short.

Like von Neumann's automaton, the Game of Life runs on an infinite, two-dimensional grid of square cells. But unlike von Neumann's automaton, each cell can be in one of only two possible states, live or dead. And each cell interacts with its eight neighbouring cells: the cells that are horizontally, vertically, or diagonally adjacent to it. After each turn of the game, the cells transition following these rules:

1. Any live cell with fewer than two live neighbours dies (as if by underpopulation)
2. Any live cell with two or three live neighbours lives on to the next generation
3. Any live cell with more than three neighbours dies (as if by overpopulation)
4. Any dead cell with exactly three live neighbours becomes a live cell (as if by reproduction)

Conway's Game of Life is a "no-player" game, just like von Neumann's automaton. The initial pattern acts as the seed of the system. And each successive generation is gotten by applying the game rules to the previous generation without any new input.

We can implement these rules in code as:

// Returns the next state of the cells applying the Game of Life rules
function next(grid) {
  // First, we create a new grid with the same
  // dimensions as the current grid
  const nextGrid = new Array(grid.length);
  for (let i = 0; i < grid.length; i++) {
    nextGrid[i] = new Array(grid[i].length);
  }

  // For each cell in the current grid...
  for (let x = 0; x < grid.length; x++) {
    for (let y = 0; y < grid[x].length; y++) {
      let c = 0;

      // For each of the cell's neighbours...
      for (let dx = -1; dx <= 1; dx++) {
        for (let dy = -1; dy <= 1; dy++) {
          if (
            // Check that we're not looking at the cell itself...
            !(dx === 0 && dy === 0) &&
            // And that the neighbour is not outside the grid
            typeof grid[x + dx] !== 'undefined' &&
            typeof grid[x + dx][y + dy] !== 'undefined' &&
            // If the neighbour is live, increment c
            grid[x + dx][y + dy]
          ) {
            c++;
          }
        }
      }

      // If the cell is live, and it has two or three live neighbours...
      // Or the cell is dead, and it has three live neighbours, it should
      // be live in the new grid.
      // If not, the cell should be dead in the new grid.
      nextGrid[x][y] = grid[x][y] ? c === 2 || c === 3 : c === 3;
    }
  }

  return nextGrid;
}

next([
  [false, false, false],
  [true, true, true],
  [false, false, false],
]);
// Returns:
//   [[false, true, false],
//    [false, true, false],
//    [false, true, false]]

Life forms ​

Many different patterns occur in the Game of Life, and we typically classify them according to their behaviour.

Still lifes are patterns that don't change from one generation to the next (as long as they are not disturbed by other patterns).

Oscillators are patterns that return to their initial state after a finite number of generations. The number of generations it takes to return to the initial state is called the pattern's period.

Spaceships can move across the board.

Methuselahs, like the R-pentomino, evolve for many generations before stabilizing.

There are more complex patterns, like stationary guns that produce gliders and other spaceships.

And it gets even more interesting. We can use glider guns as digital signal generators, construct logic gates (like AND, OR, and NOT gates) and memory blocks based on the interactions of gliders, and combine these logic gates and memory blocks to create patterns that can perform computations. In fact, the Game of Life is Turing-complete. In theory, it can simulate any computation that a typical computer can perform—including simulating itself!

Remember John von Neumann's vision of machines that can replicate themselves? Different patterns in Life have been developed that make copies of themselves. One, called Gemini, creates a copy of itself while destroying its parent. Another, the linear propagator, which has a bounding box with 15 million cells on each side, creates a complete copy of itself in 237 million generations while retaining its parent.

On the surface, the Game of Life is an interesting mathematical game and a fun programming exercise. But Life illustrates something even deeper. Against our intuitions that complex things must arise out of even more complex things, it shows how complexity and organization can emerge from simplicity. Life, as it turns out, is more than just a game.

Check out the online demo for Conway's Game of Life and the source code on GitHub.